NTP Leap Smearing Test Results
Starting with v4.2.8p4, the NTP daemon ntpd in the role of a server is capable of smearing the time sent to clients when a leap second is about to be inserted.
This forces other instances of ntpd in the role of a client of that server to adjust their time gradually over a certain interval,
and prevents the clients from stepping their system time back to account for a leap second, which could cause severe problems with applications.
If usage of any leap smearing approach is considered in general it should be determined first if this is at all suitable for an application. More basic information as well as pros and cons can be found here:
In some forums and mailing lists there have been discussions
- How long the smear interval should be
- If time smearing should be done in a linear way, or in a cosine or another non-linear shape
- If time smearing should be finished at the end of the leap second, or half of the smearing should occur before and the other half after the the leap second
While the last question is more a question of policy, the first 2 points determine if a client is at all capable of following the smeared time, and how much a client's time deviates from the server time around the smear interval.
The latter depends on the interval at which a client polls the server. Obviously, if the polling interval is short then the client detects the increasing smear offset earlier than a client with a large polling interval.
Currently the standard implementation of ntpd supports only smearing using a cosine shape in a way that it is finished at the end of a leap second.
For the tests the source code was modified so that alternatively a linear smear offset could be applied.
NTP Clients with Fixed Polling Interval
The initial tests were run using a smearing NTP server, and 3 clients with polling intervals fixed to 4 (16 s), 6 (64 s), and 10 (1024 s). All machines running ntpd 4.2.8p8 under Linux. Individual tests were made with cosine and linear smear, and smear intervals of 1 day (86400 s), 2 hours (7200 s), and 2000 s.
In the graphs below the smear offset starts at 0 at the beginning of the smear interval, and goes to -1000 ms at the end of the interval, which is coincident with the end of the leap second.
- red dashed line: smear offset provided by the server
- green lines: measurements of the client with poll 4
- blue lines: measurements of the client with poll 6
- violet lines: measurements of the client with poll 10
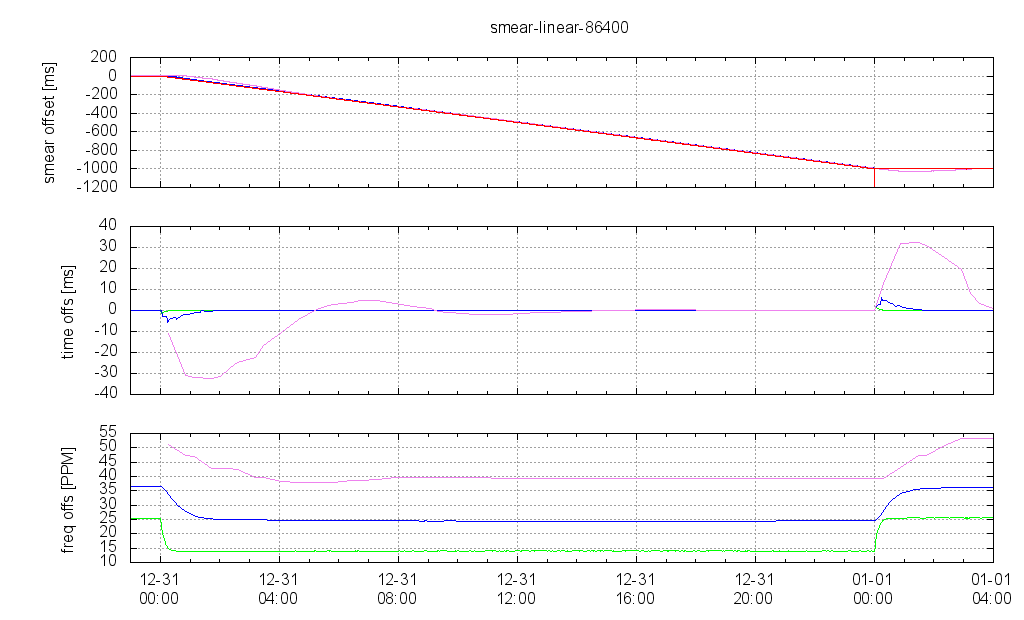
Leap Smear Over 24 Hours
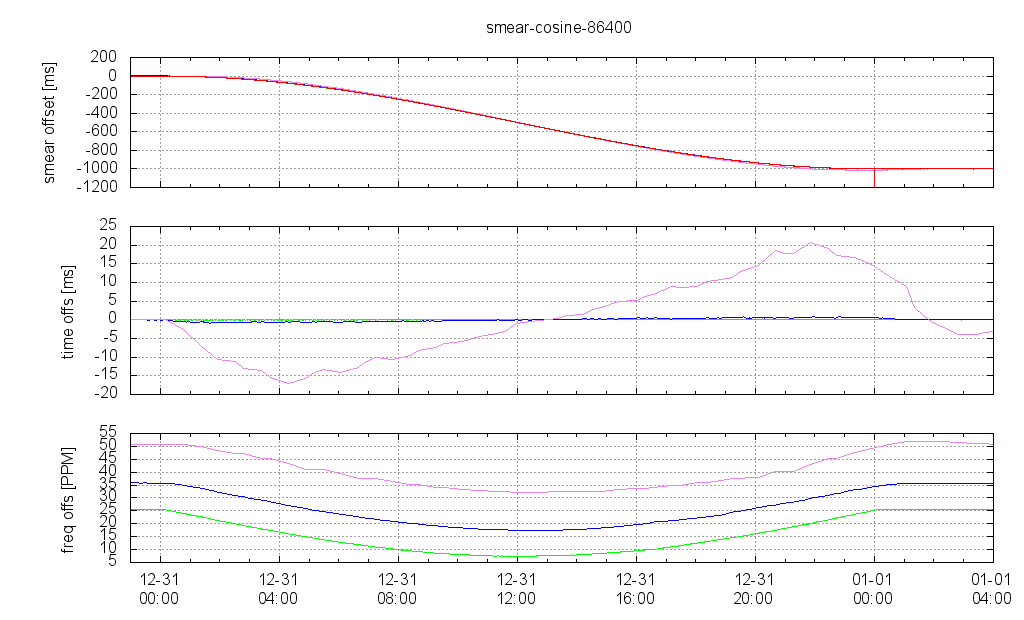
If smearing is done over 24 hours then all clients have sufficient time to follow the increasing offset of the server time. According to the generated loopstats files the highest difference to the server time is 20 ms with poll 10 (violet), while poll 6 (blue) yields < 1 ms, and poll 4 (green) even < 0.1 ms.
Compared to the cosine approach where smearing starts slowly, then increases over time, and finally fades out, the maximum time offset is higher if smearing is done with a linear shape, where the time suddenly starts to drift at a constant rate. The maximum time deviations are < 32 ms for poll 10, < 6 ms for poll 6, and < 1.5 ms for poll 4.
An interesting observation here is that with a cosine smear the correction of the time offset at the end of the smear interval already starts at, and has its maximum quite some time before the end of the interval. When smearing stops the time offset is already decreasing, and even with poll 10 it is only about 15 milliseconds at the end of the smear interval.
With the linear approach the clock drift doesn't change until smearing ends, so the client's time offset to the server is close to 0 at the end of the smear interval, but then starts to rise, and reaches its maximum quite some time after smearing has already been finised. In case of poll 10 the maximum time offset is 32 ms about 1.5 hours after smearing has been finished.
The frequency offset shift during the smear is -12 ppm for linear approach, constantly over the smear interval, and a sine shape with -18 ppm maximum for the cosine approach.
Leap Smear Over 2 Hours
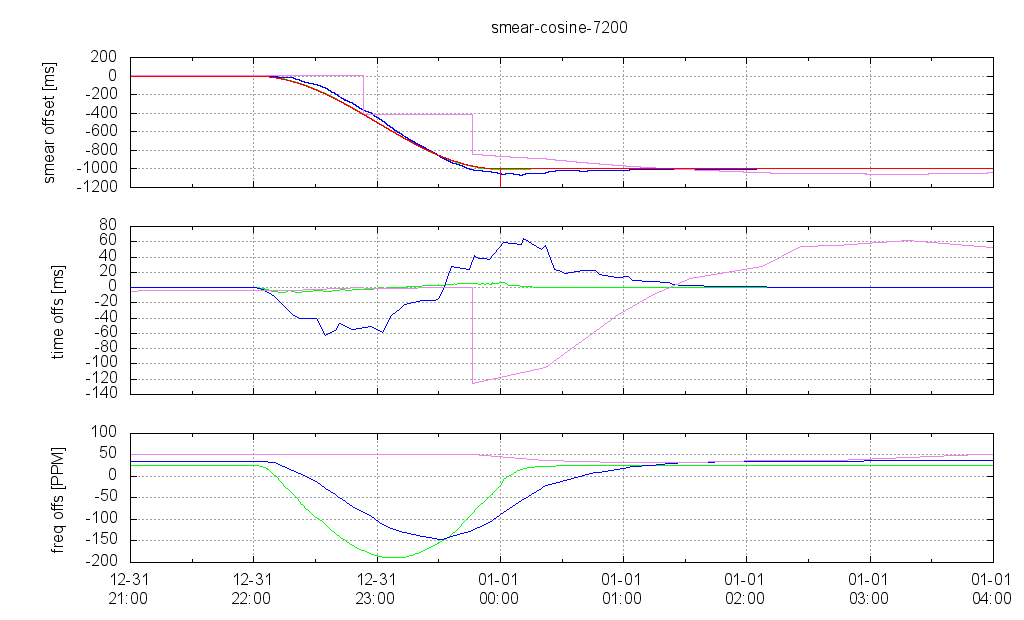
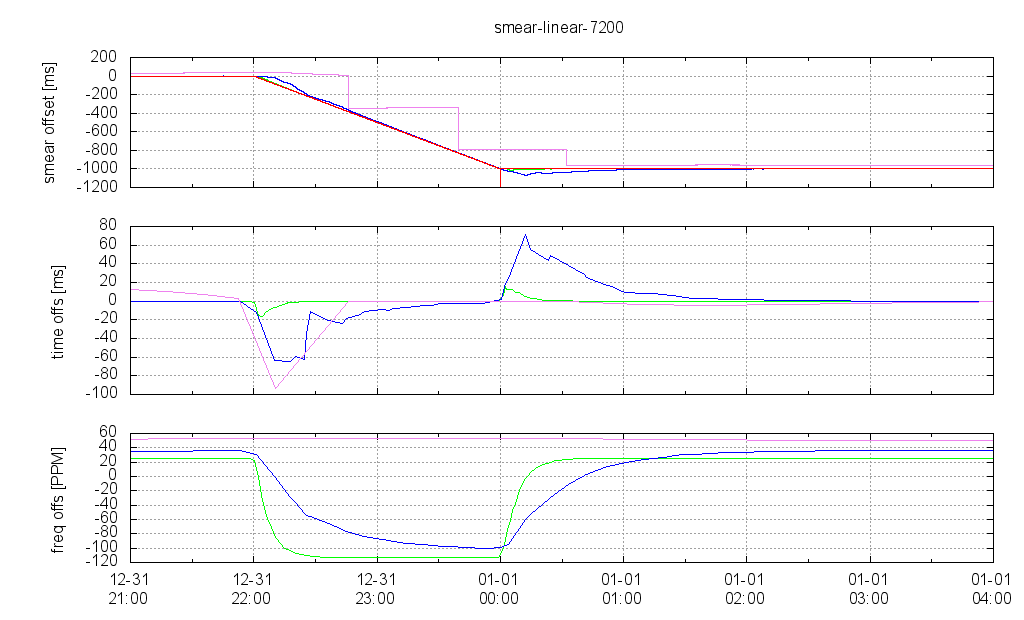
If smearing is done over 2 hours only then obviously larger time deviations evolve during a poll interval. The client with poll 4 (green) can still easily follow the smeared time from the server, with small maximum time deviation, but the client with poll 6 (blue) has now a maximum time deviation of 60 ms and it takes about 1.5 hours after the end of the smear interval until the client's control loop has settled again and the time offset is as low as usual.
The client will poll 10 (violet) totally fails to follow up with the server time, and steps its time back several times during the smear interval, twice with the cosine approach end even three times with the linear approach. So what we tried to avoid with the smear approach happens even more often if the smear interval is too short.
The frequency offset is significantly larger than with the longer smear interval since the same amount of time has to be slewed during a shorter interval.
Leap Smear Over 2000 Seconds
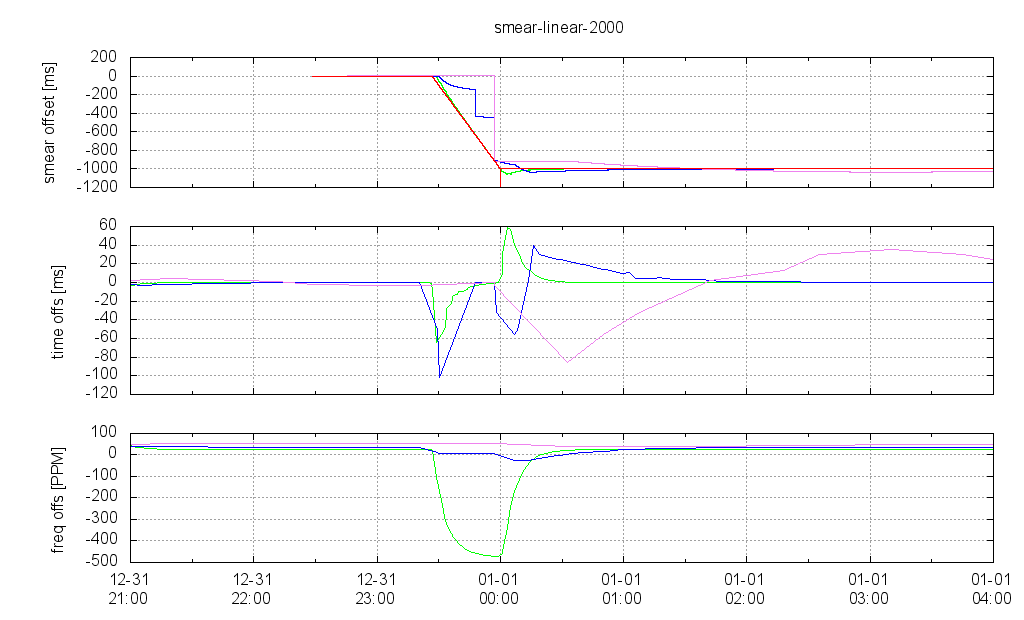
Smearing over 2000 seconds only yields the worst results at all. Only the client with poll 4 (green) is capable of following the smeared server time. Even though the maximum time deviation is only about 60 ms, the maximum frequency shift is close to -500 ppm, which is a slew limit built into ntpd and some Unix kernels.
Even the client with poll 6 (blue) steps the time backward 2 times. The client with poll 10 (violet) steps the time back only once. With a polling interval of 1024 s the smear interval of only 2000 s looks mostly similar to a simple time step back by the server, so this client behaves mostly the way it would behave with a non-smearing server.
NTP Clients With Variable Polling Interval
The next tests were run with an NTP server smearing the leap second over 10 hours, and 3 clients synchronizing to that server. All machines running Linux.
For this test the clients' polling intervals were not fixed, and the tests started early enough that the clients had a chance to increase their polling interval up to 10. This corresponds to a standard situation where the server and the clients have been running continuously. The question is how these clients behave when they poll the server next time after the server has started smearing, and determine that the time offset has unexpectedly increased since the last poll.
Again, in the graphs below the smear offset starts at 0 at the beginning of the smear interval, and goes to -1000 ms at the end of the interval, which is coincident with the end of the leap second.
The graphs include the “smear offset” of the time delivered by the server and each client as well as the “time offset”, “frequency offset”, and also the “poll” interval from each client's loopstats file.
- red dashed line: smear offset provided by the server
- green, blue lines: measurements of two clients running ntpd 4.2.8p8
- violet line: measurements of one client running ntpd 4.2.6p5
Cosine Smear Over 10 Hours
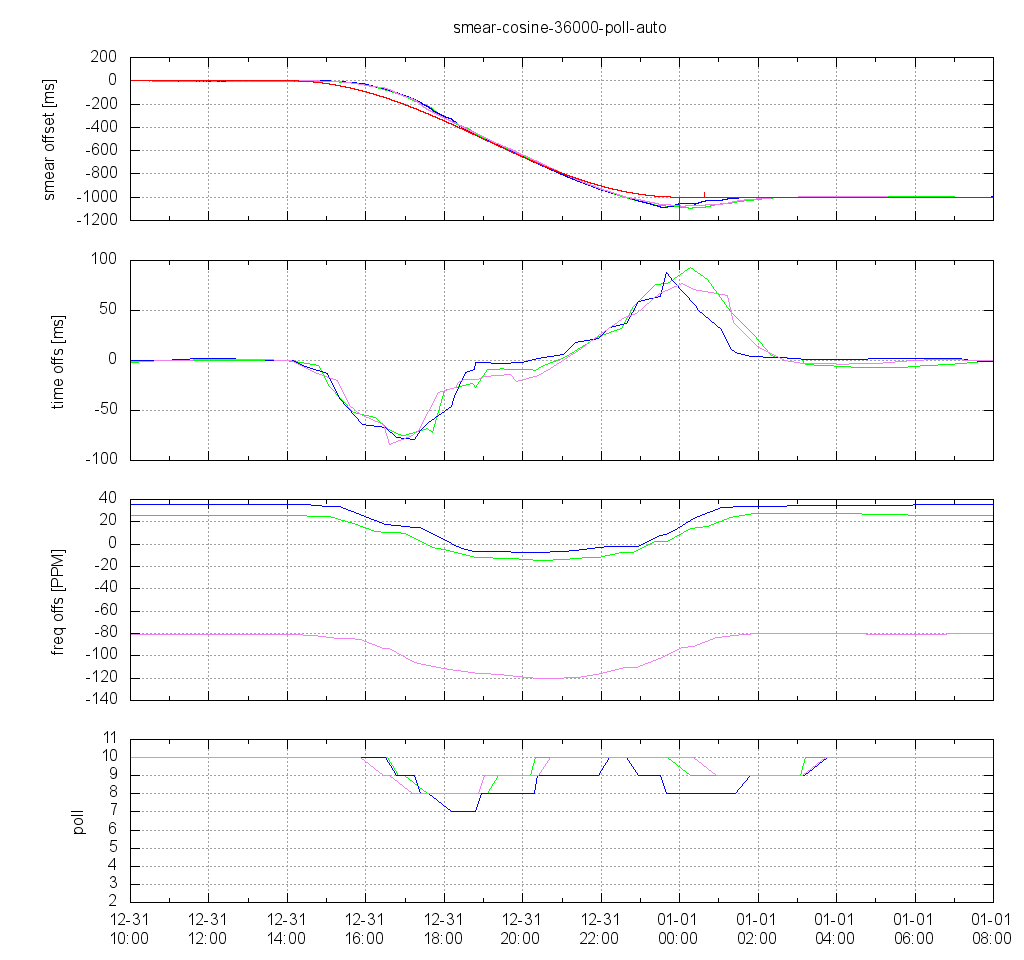
The clients decrease their poll interval when they detect that the time offset has increased since the last poll due to the beginning of the smearing. However, the poll interval decreases only slowly since smearing starts slowly, and thus the frequency offset starts to increase slowly. In the middle of the smear interval the frequency offset stays nearly constant, so the clients start to increase the poll interval again. Near the end of the smear interval the frequency offset changes faster again, and thus the poll interval is decreased again.
It should be noted that the smear interval is only decreased to 8 or sometimes 7, but not below that. Just like observed earlier, the time offset occurring at the end of the smear interval starts and reaches its maximum quite some time before smearing ends, but it still takes nearly 3 hours after the end of the smear interval until the clients' time offset have settled.
Linear Smear Over 10 Hours
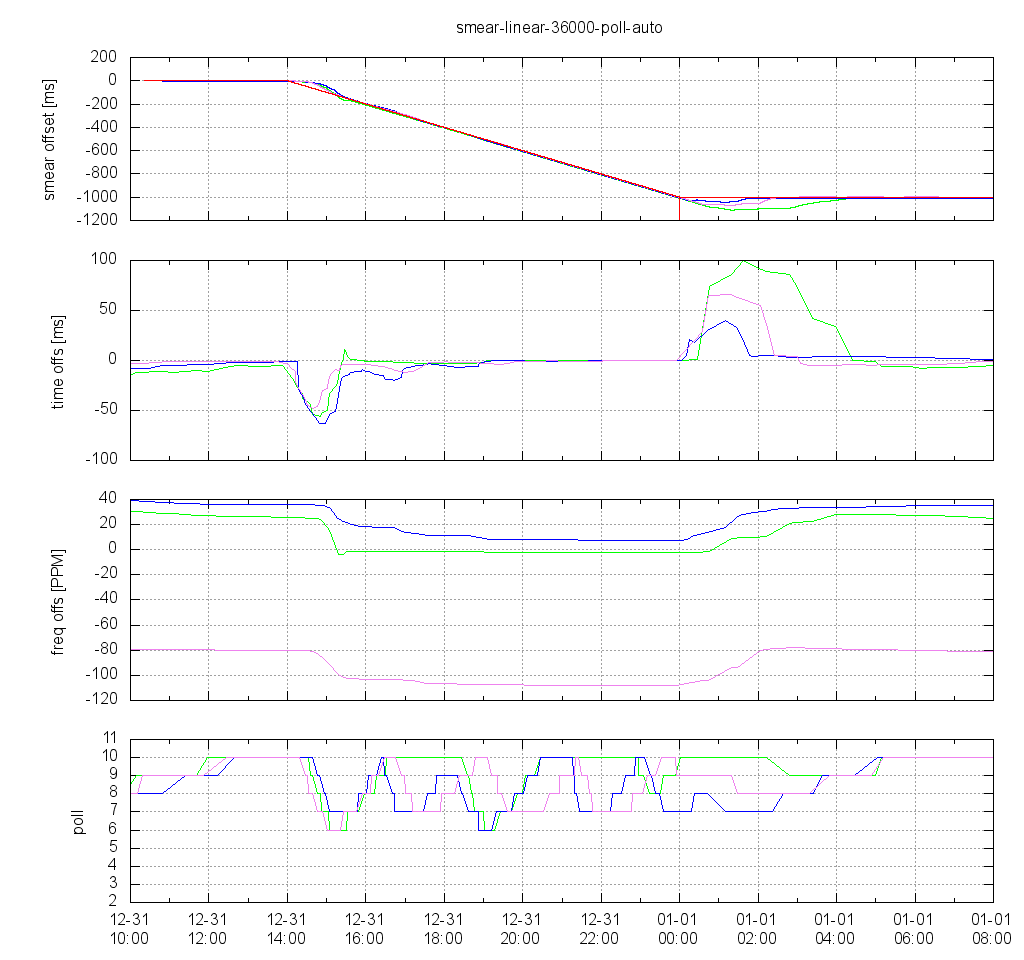
The clients decrease their poll interval when they detect that the time offset has increased since the last poll due to the beginning of the smearing. At the beginning of the smear interval the frequency offset changes faster with the linear smear than with the cosine shape, so the clients decrease their poll interval more than with the cosine approach. The poll interval decreases to 7 or even 6, which results in a faster reaction to the frequency change, and thus the resulting maximum time offset is smaller than with the cosine approach.
During the smear interval the polling interval ramps up and down several time, and as already observed in the earlier tests, the time offset due to the frequency change at the end of the poll interval starts and reaches its maximum value only after smearing has already been finished, and it takes nearly 5 hours until the clients' time offset have settled.
Let A Smearing Server Suggest A Poll Interval
In an email discussion how the client behavior could be improved, the maintainer of the NTP project, Harlan Stenn, made a suggestion that an NTP server could send a small poll value in the reply packets sent to its clients. Normally a client puts its current poll value (e.g. 6 or 10) into the request packet sent to a server, and the server copies this value into the reply packet.
Harlan Stenn's original idea was to let the server put a low poll value (e.g. 3 or 4) into the reply packets already some time before smearing starts, so that clients already decrease their poll interval before the server starts smearing, and can follow the smeared time very quickly.
However, for these tests a simple ntpd's source code was only slightly modified so that it puts poll 4 into the reply packets just during the smear interval, so clients running with poll 10 might still receive the first such reply 1024 seconds after smearing has started.
For large installations it must be kept in mind that with such an approach the number of requests which need to be handled by the NTP server increases significantly over a leap second smear. For example, 8000 clients with poll interval 6 (64 s) will cause a mean load of 125 req/s, but if all these clients change their poll interval to 4 (16 s) then the request rate to be handled by the server increases to 500 req/s.
Cosine smear Over 10 Hours, Server Suggests Poll 4
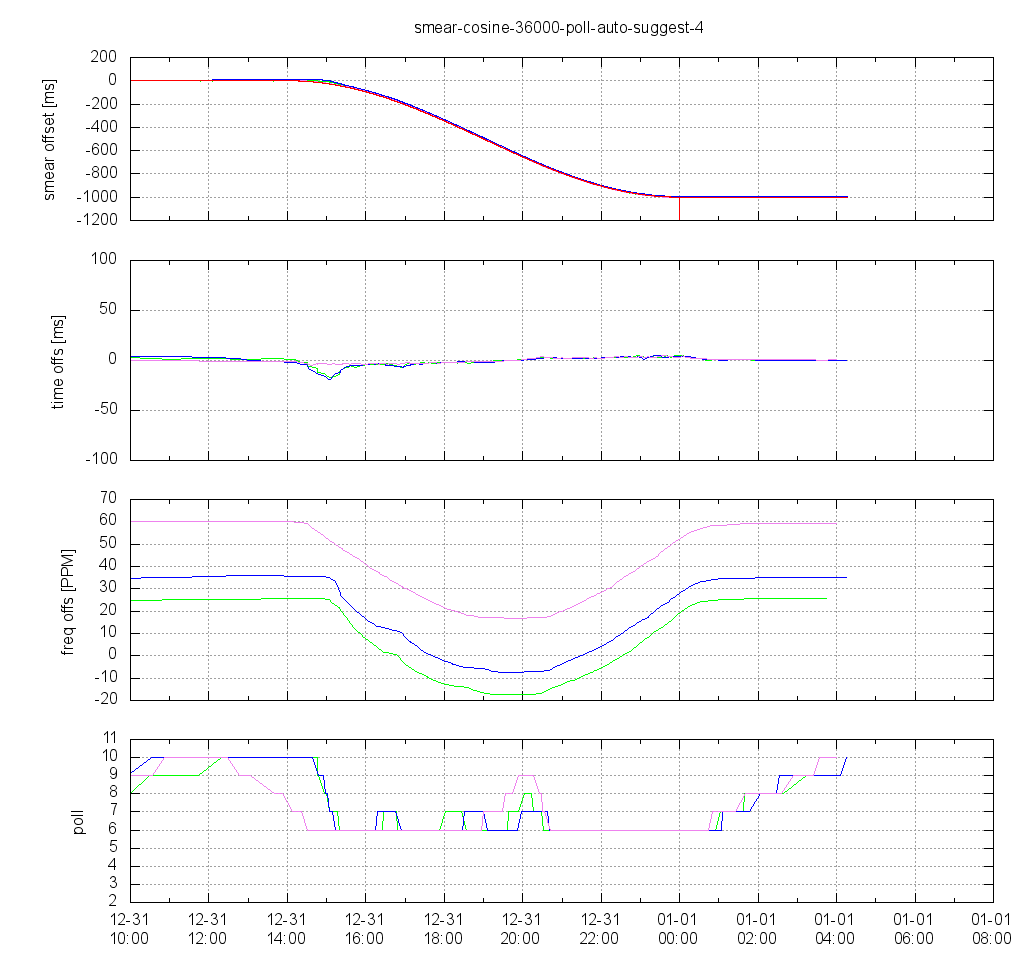
The first test was run with a cosine smearing shape. For some reason the 4.2.6p5 client (violet) already started to decrease his poll interval already before the server started sending poll 4. Eventually the reason is that ntpd hasn't been running long enough before to stay at poll 10. Anyway, both 4.2.8p8 clients decrease their poll interval quickly after smearing has started. The interesting thing here is that, even though the server suggests poll 4, the clients decrease their poll interval only down to 6, which corresponds to the default minimum poll interval. Also, the poll interval increases a little bit in the middle of the smear interval, even though the NTP server continuously sends “poll 4” to the clients. It has to be checked in ntpd's source code why this is the case.
The time offset reported in the loopstats file stays pretty small over the whole smear interval. There is no significant time offset at the end of the smear interval, and the client's poll intervals increase slowly again after smearing has finished.
Linear smear Over 10 Hours, Server Suggests Poll 4
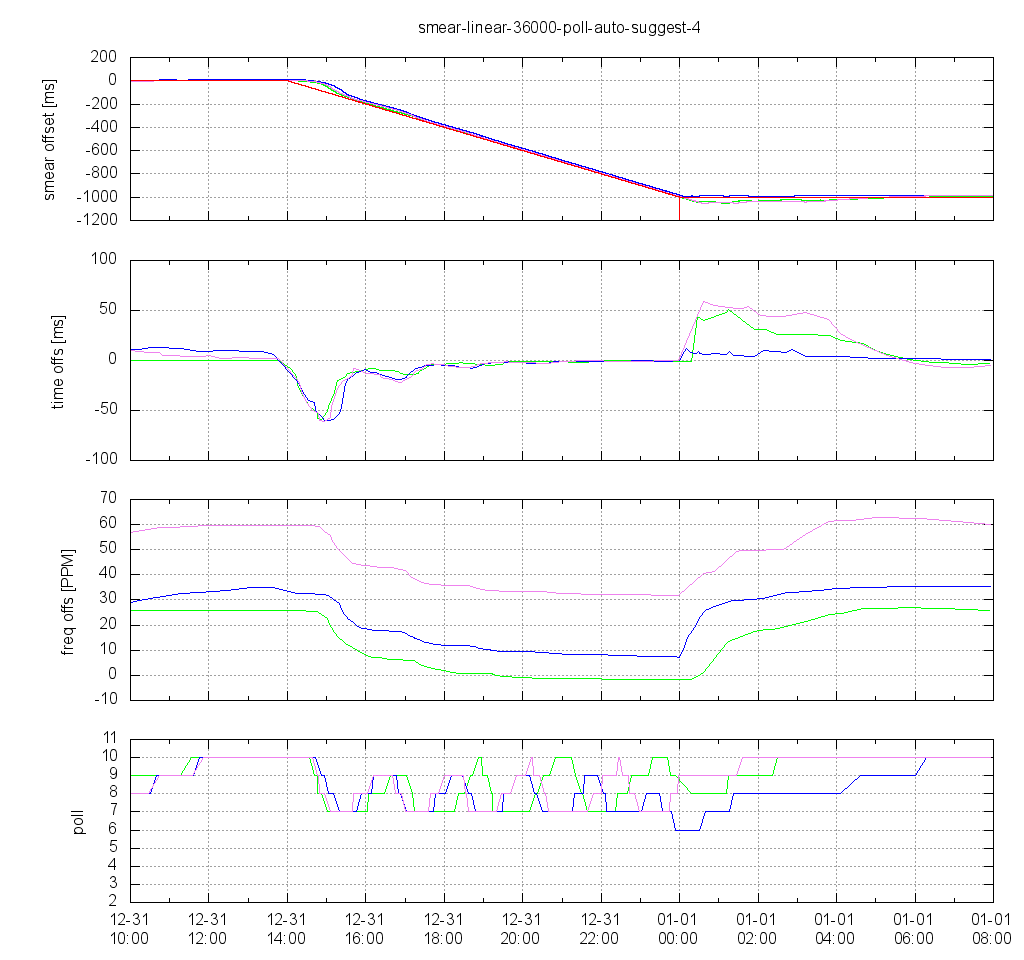
A test with a linear smear shows that the clients also decrease their poll interval quickly when the server starts smearing and sending “poll 4” in the reply packets. However, during the smear interval the clients' poll value increases and decreases several time, which is presumably due to the same reasons why the suggested poll interval isn't simply accepted, and limited to 6.
At the end of the smear interval the same thing happens as in the earlier tests: The sudden frequency change at the end of the linear slope causes an increasing time offset which needs to be corrected, and depending on whether the current poll interval at this time is low (e.g. 6) or higher (e.g. 9) the maximum time offset is lower or higher, and the time until the offset has settled is short or significantly longer.
Conclusion
Basically, the smear interval should be as long as possible. Short smear intervals can cause clients to step the time backward, which should actually be prevented by a smearing approach.
With the current ntpd versions the cosine smear yields smoother results than the linear smear, i.e. a lower maximum time deviation from the server. The continuously changing frequency offset lets the clients decrease their polling interval and react faster to changes. Especially at the end of the smear interval the time offset settles faster with a cosine shape than with a linear smear.
A possible improvement at the server side as suggested by Harlan Stenn is to let the server send a low poll value to its clients during the smear interval. If the server started doing so already before smearing starts then clients would have decreased their poll interval already when smearing starts, which should significantly reduce the time offset between the clients and the server at the beginning of the smear interval.
A question is why the client ntpds indeed seem to decrease their poll value if the server sends a lower poll value, but on the other hand don't go below the default minpoll value (6), and even start to increase their polling interval afterwards even though the server still sends a small poll value. Looks like here is room for improvements in the role of a client.
Whether smearing is to be done completely before the end of the leap second, or partly before and partly after the leap second is mainly a question of policy.
The advantage of the former approach is that smearing is finished at the end of the leap second, so the time matches UTC at the beginning of the next day / hour / minute, but the time offset from UTC is maximum -1 s immediately before the leap second.
The latter approach has the advantage that the maximum time offset from UTC is only 0.5 s, but the time doesn't match UTC immediately after the leap second. Which approach is more appropriate, and if smearing is suitable at all, depends on the applications running on the clients.
— Martin Burnicki 2016-12-23 01:25